Êlektron

Impédance

1 - Définition

Inertie opposée par un système, ou par un milieu, au passage d'un phénomène périodique. L'impédance s'exprime par un nombre complexe, noté Z, égal au rapport entre l'amplitude complexe du phénomène cause et l'amplitude complexe du phénomène effet, les deux phénomènes étant supposés de même fréquence.
La partie réelle de Z s'appele résistance R, sa partie imaginaire s'appelle réactance, X. Selon que le phénomène résultant est en avance ou en retard sur le phénomène initial, la réactance prend le nom d'inductance ou de capacitance.
La grandeur Y=1/Z, inverse de l'impédance, est l'admitance. Sa partie réelle est la conductance C, sa partie imaginaire est la susceptance S. Toutes ces grandeurs sont liées entre elles.

Plus simplement l'impédance électrique mesure l'opposition (la résistance) d'un circuit électrique au passage d'un courant alternatif sinusoïdal.
En courant alternatif sinusoïdal, on ne parle pas de résistance mais d'impédance et la loi d'Ohm s'écrit : U_eff = Z.I_eff

Où U_eff est la tension efficace (en volts) mesurée aux bornes du dipôle d'impédance Z (en ohms) traversé par le courant d'intensité efficace I_eff (en ampères)

2 - Nature de l'impédance

Une impédance Z est en fait l'association en série (ou en parallèle) d'une résistance R et d'une réactance X.

La réactance X peut être capacitive (X_C) ou inductive (X_L) selon qu'elle est due à une capacité (capacité parasite ou condensateur) ou une inductance (self parasite ou bobine).

Si capacité et inductance cohabitent, ce qui est toujours le cas en pratique, on considèrera seulement la somme algèbrique des deux valeurs en affectant à X_C un signe négatif et à X_L un signe positif.

Exemple :

A une fréquence donnée, la réactance d'un dipôle (équivalente à un condensateur) est de 18 ohms tandis que celle de la self en série avec ce dernier est de 12 ohms. La réactance X équivalente à cette association est égale à : X= (-18) + (+12) = -6 ohms. C'est donc une réactance capacitive puisqu'elle est négative.

3 - Représentation de Fresnel

Prenons le cas d'un dipôle formé d'une résistance pure R en série avec une réactance C pure (condensateur sans perte ou bobine de résistance nulle).
Ici, il s'agit d'une bobine.

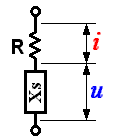
Image d'un dipôle formé d'une résistance pure R en série avec une réactance X pure

Lorsqu'un signal sinusoïdal est appliqué aux bornes du dipôle, on peut visualiser à l'oscilloscope la tension u aux bornes de la réactance Xs. Le courant qui traverse cette dernière se traduit par une tension i aux bornes de la résistance R

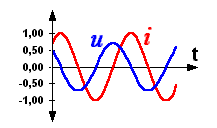
Image de la courbe et du courant déphasés de 90°

Sur l'écran de l'oscilloscope bicourbe s'affichent simultanément la tension aux bornes de la réactance, en avance de 90 degrés sur l'intensité du courant dans le dipôle (matérialisée par la tension aux bornes de R grâce à la loi d'Ohm).

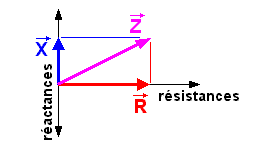
La tension u et l'intensité i sont déphasés de 90 degrés. Les vecteurs X et R forment pour cette raison un angle de 90 degrés.
Le vecteur Z, qui représente l'impédance, est la somme des vecteurs X et R.
On peut calculer son module, c'est à dire la valeur en ohms de l'impédance, en utilisant le théorème de Pythagore.

Suite...